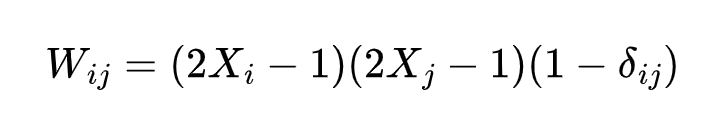Objectives
- Analog circuit models of larger neural systems
- Extending VMM+WTA concept
- Population of interconnected neurons
- Hopfield Networks
Class Schedule and Video Viewing
|
Date
|
Class Topic
|
On-Line Lectures
|
Reading Material
|
White Boards
| |
Mar 5
|
|
Diffusor I,
Diffusor II,
Diffusor III,
Dendritic Cable Modeling,
.
|
|
1,
2,
3,
4,
5,
6,
7,
8,
| |
Mar 7
|
|
|
|
1,
2,
3,
4,
5,
| |
Mar 12
|
|
|
|
1,
2,
3,
4,
| |
Mar 14
|
|
|
|
1,
2,
|
Course Materials
Reading Material
- Connecting FPAA neurons with synapses (Natarajan, Hasler, ISCAS 2019) .
- Silicon diffusors (Boahen, Andreou, NIPS 1991) .
- Diffusor as a Current DAC (Yanh,et al,ISCAS 2012) .
- Silicon, reconfigurable dendrites (Nease,et al,TBIOCAS 2012) and (Farquhar,Abramson,Hasler,ISCAS 2004)
- HMM classifier using coincidence detection in dendrites (George,et al,JPLEA 2013) .
Experiment 1: Differential VMM WTA Decision Boundaries
Last project, we explored the VMM WTA circuit as a single layer classifier where positive only inputs and details of the implementation were provided. However it was designed to classify a single output (XOR) with the other boolean gate classification being incidental. This project, we delve into differential input schemes and constructing decision boundaries for all 3 outputs as seen in the VMM WTA paper .
(a) Differential Input Scheme
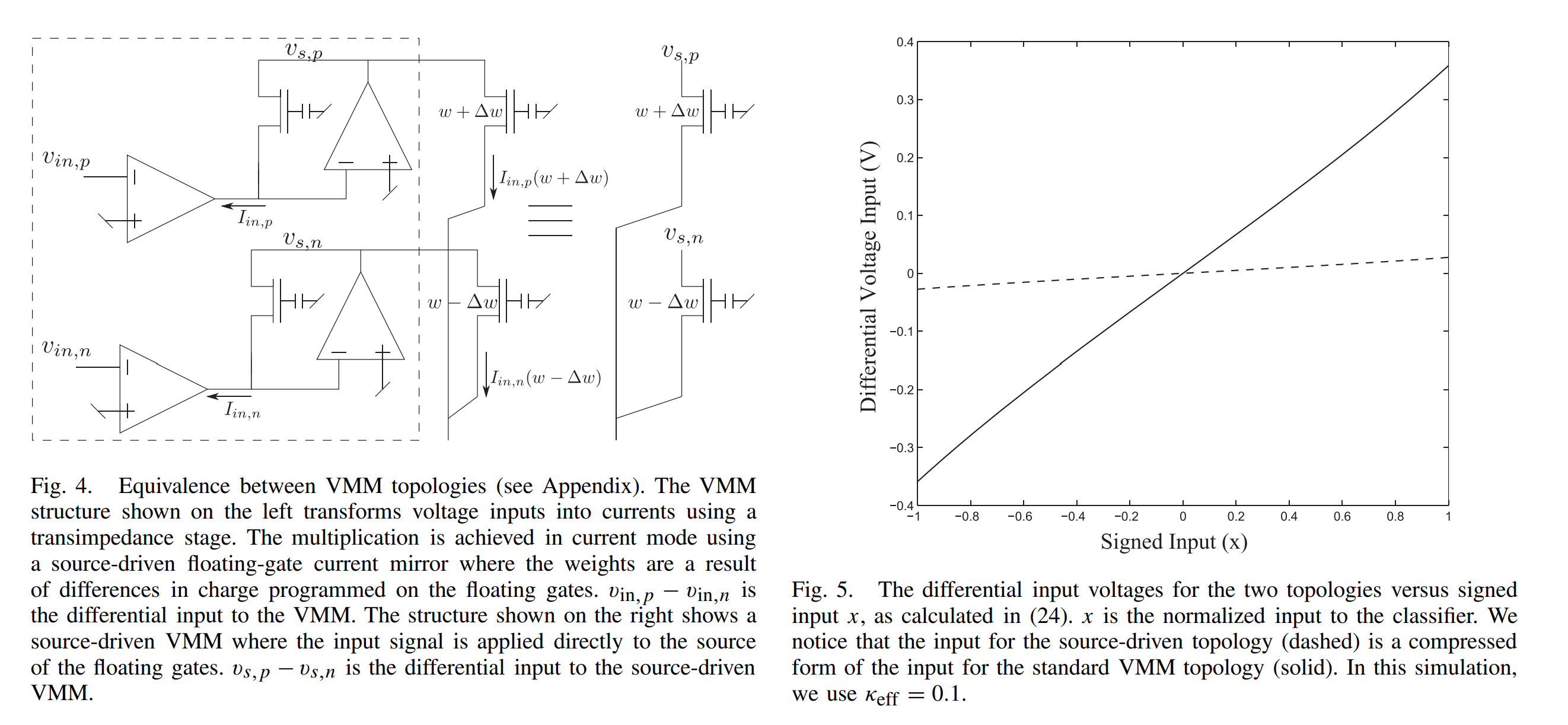
- Using either the vmm 2x3 circuit or a custom macrocab, construct and measure a differential input scheme similar to the dashed line above.
- Explain how your reference or 'zero' voltage is set and how you are able to use the weights of the matrix to set output voltages above and below that.
(b) Multi Class Decision Boundaries

- Using a programming language of your choice (matlab, python etc) simulate a signed-input weight matrix and generate the plot on the left in the figure above.
- Implement and measure the output of a 2x3 VMM WTA network with similar boundaries as the figure on the right.
Experiment 2: The Hopfield Network
The Hopfield network, inspired by the interconnected structure of neural systems, can "remember" patterns through a Hebbian learning rule and attractor dynamics (Hopfield, PNAS 1982) .
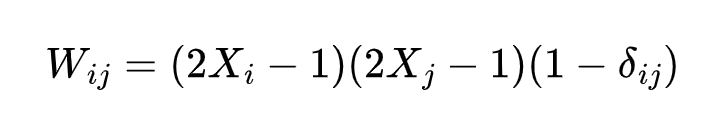
- Choose a 4-bit pattern for your 4-neuron Hopfield network to remember (ex. 1111,1001, ....)
- Using the Hebbian learning rule, find the weights that encode your 4-bit pattern into the Hopfield network
- Relate the Hebbian learning rule to neural adaptation
The Hopfield analog circuit uses Transconductance Amplifiers (TAs) for the sigmoidal activation function and a Floating-Gate Vector-Matrix-Multiply (FG-VMM) to sum weighted inputs to a neuron (Mathews, Hasler, ISCAS 2023) .
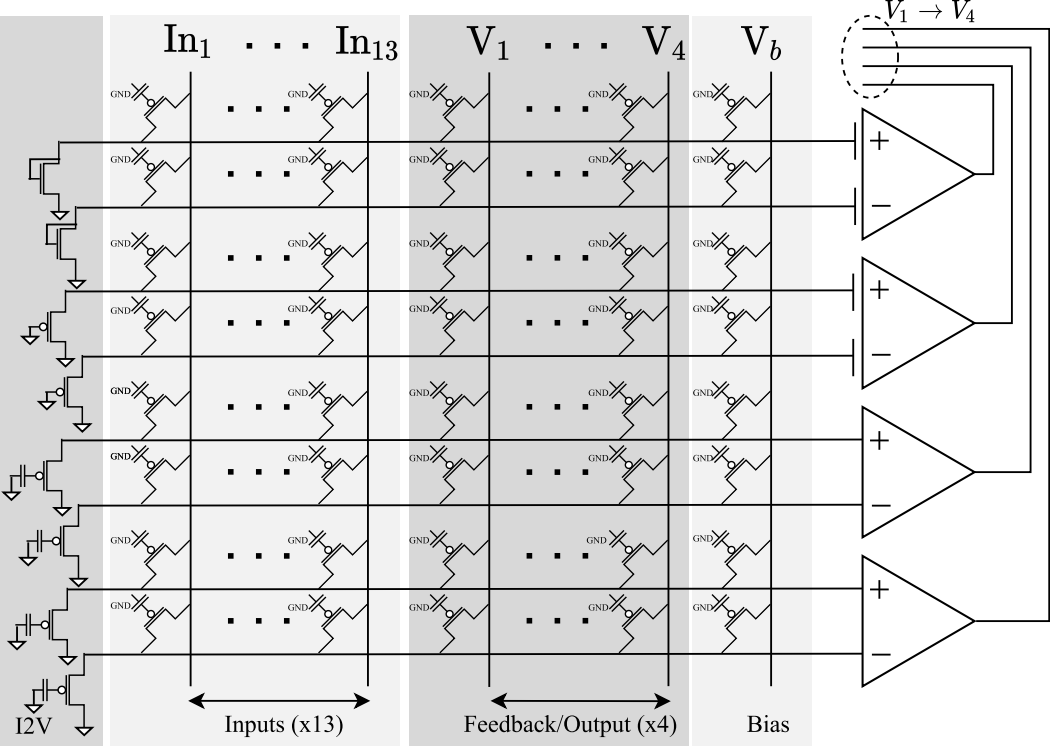
- Program a Hopfield network on the FPAA
- Scale your weights calculated previously into currents (Wij = 1 -> Wij = 25 nA)
- Measure the network converging from two different unstable starting conditions
- Does it converge as expected? Why or why not?
- Relate your observed network behavior to neural systems
|