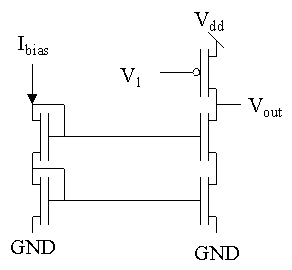
Problem #2: MOSFET Amplifier with a current source bias

A MOSFET Amplifier with a current source bias. For these matched nFET and pFET devices, Kn = 32
mA / V2, Kp = 10 mA / V2, and VT = 1V, Ith = 0.2 mA, VA = 25V for both nFETs and pFETs.We calculated the capacitances for you: Cgd = 2fF (both nFET and pFET, operating in saturation) Cgs = 20fF (both nFET and pFET, operating in saturation) Cdb = 4fF (both nFET and pFET, operating in saturation) Csb = 6fF (both nFET and pFET, operating in saturation)
(a) Draw the low-frequency small-signal for this circuit and calculate the low-frequency parameters for the pFET devices. Iref is 1.25
mA.Answer: We have a cascode current source, and we know that it's small signal model is an output resistance, which is equal to the bottom bias transistor multiplied by the open-loop gain of the cascoding transistor.

1.25
mA = ( (Kp = 10 mA / V2 )/ 2) ( Vsg - VT)2Therefore, Vsg - VT = 500mV.
gmp = 2(1.25
mA) / 500mV = 5 mA / V = 1 / (200 kOhms)ron = rop = VA / 1.25
mA = 20 Mohms(b) Calculate the gain from input to output and the output resistance of this circuit.
Gain = gmp rop = 2 (25V) / 500mV = 100 (the output resistance of the nFET device is huge)
Rout = rop = 20 Mohms
(c) Draw the new small-signal model taking into account capacitors. Calculate the frequency response (i.e. calculate the corner frequency(s) ) of this circuit assuming the input is driven by an ideal voltage source.
We have one capacitor from the output to a.c. ground composed of three capacitors:
Cout = Cgd,n + Cdb,n + Cdb,p = 10fF
We also have the feedback capacitor: Cgd,p = 2fF.

Using the Miller theorem, Cgd,p becomes a capacitor of size Cgd,p between the output voltage and ground (the miller multiplied capacitance would appear at the gate input, and since it is being driven by an ideal voltage source, we don't experimentally see this effect). This approximation will ignore capacitive feedthrough at very high frequencies (at the signal gain equal to 1/6).
The total capacitance is a single capacitance at the output, CL = Cout + Cgd,p = 12fF
As a result, the frequency response is a first-order low-pass filter with the corner frequency at
fcorner = gm / (2
p CL ) = 1 / (2p (200 kOhms) 12fF) = 66.3 MHzMore accurately, one would have to model the drain-source region between the nFET current source transistor and the nFET cascoding transistor, since that will have some effect on the answer (actually, it improves the output resistance which is already large, and therefore even more negligable).