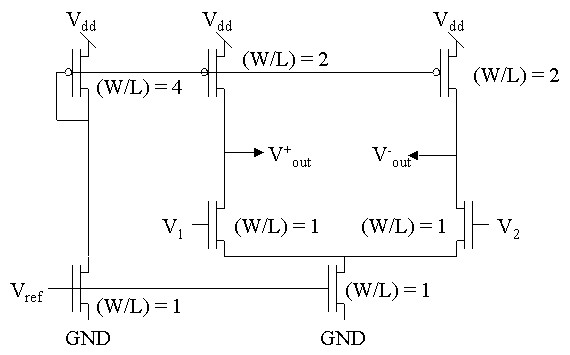
Problem #3: A MOSFET Differential Amplifier Problem
A MOSFET based differential amplifier. Assume all nFETs and pFETs are matched to each other with the (W/L) ratios as shown. Assume Vref sets a bias current of 2
mA to the nFET current source transistors when biased in saturation.Further, K'n = 32
mA / V2, K'p = 10 mA / V2, and VT = 1V, Ith' = 0.25 mA, VA = 25V for both nFETs and pFETs.(a) What is the bias currents flowing through the differential-pair transistors? Are any of the pFETs in the ohmic region?
Bias currents = 1
mA for each transistor. All pFETs are in saturation.(b) Draw the Small-signal Model for this differential amplifier assuming a common-mode signal applied to V1 and V2, and then the small-signal model for a differential signal applied to V1 and V2. Solve for the small-signal parameters.

1
mA = ( (K'n = 32 mA / V2 )/ 2) ( Vgs - VT)2Therefore, Vgs - VT = 250mV.
gm = 2(1
mA) / 250mV = 8 mA / V = 1 / (125 kOhms)ron = rop = 2 rob = VA / 1
mA = 25Mohms; ron // rop = 12.5Mohms(c) Solve for the differential, common-mode gain, and the common-mode rejection ratio for this amplifier.
Common-mode gain: (r0n // r0p) / (2 r0b ) = 1/4
Differential-mode gain: gm (r0n // r0p) / 2 = 50
CMRR = gm r0b = 200
(d) What is the common mode and differential mode gain if Vref sets a bias current of 0.25
mA to the nFET current source transistors?Independent of subthreshold or above threshold, ron = rop = 2 rob
Therefore, Common-mode gain: (r0n // r0p) / (2 r0b ) = 1/4 independent of subthreshold or above threshold regime.
gm = (Iref / 2) / UT ; ron = rop = VA / (Iref / 2).
Therefore, Differential-mode gain: gm (r0n // r0p) / 2 = VA / (2 UT ) = 500
(e) What practical issues make this implementation difficult to use?
Transistor Matching: a slight mismatch could leave one or many transistors in the ohmic region.