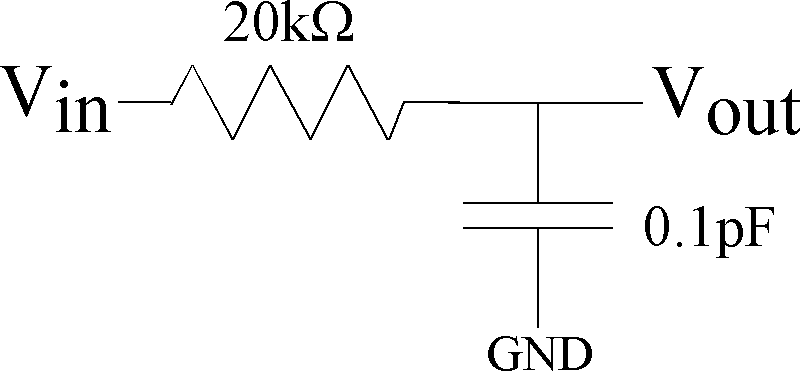|
This project primarily gets the students comfortable with measurement and resulting analysis of
time-domain (Resistor-Capacitor) circuits.
|
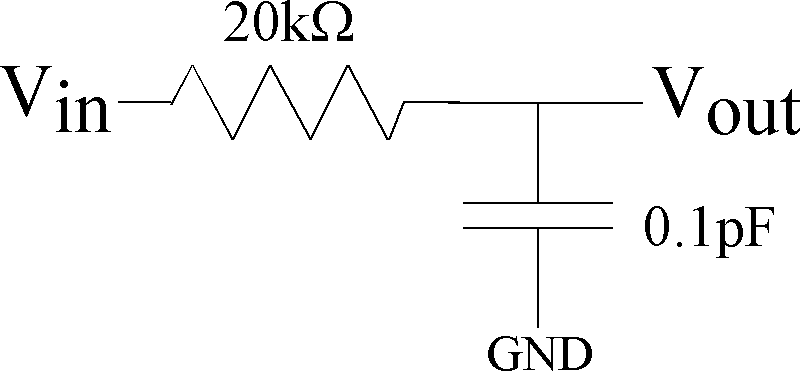
Figure 1: First-order Resistor--Capacitor Circuit for lab measurement.
The precise values of the Resistor and Capacitor are not essential,
e.g. 0.1pF may not be an ideal choice.
One should choose proper values to see the dynamics
using your particular data aquisition system.
|
Remember plots and data analysis are done in MATLAB / Scilab;
please don't include your code in your writeup.
You will submit one writeup per group electronically to the professor
(both individuals may submit the same report twice in Canvas if both names are on both documents).
Preferred naming of the submitted document: "Project2_LastName1_LastName2".
|
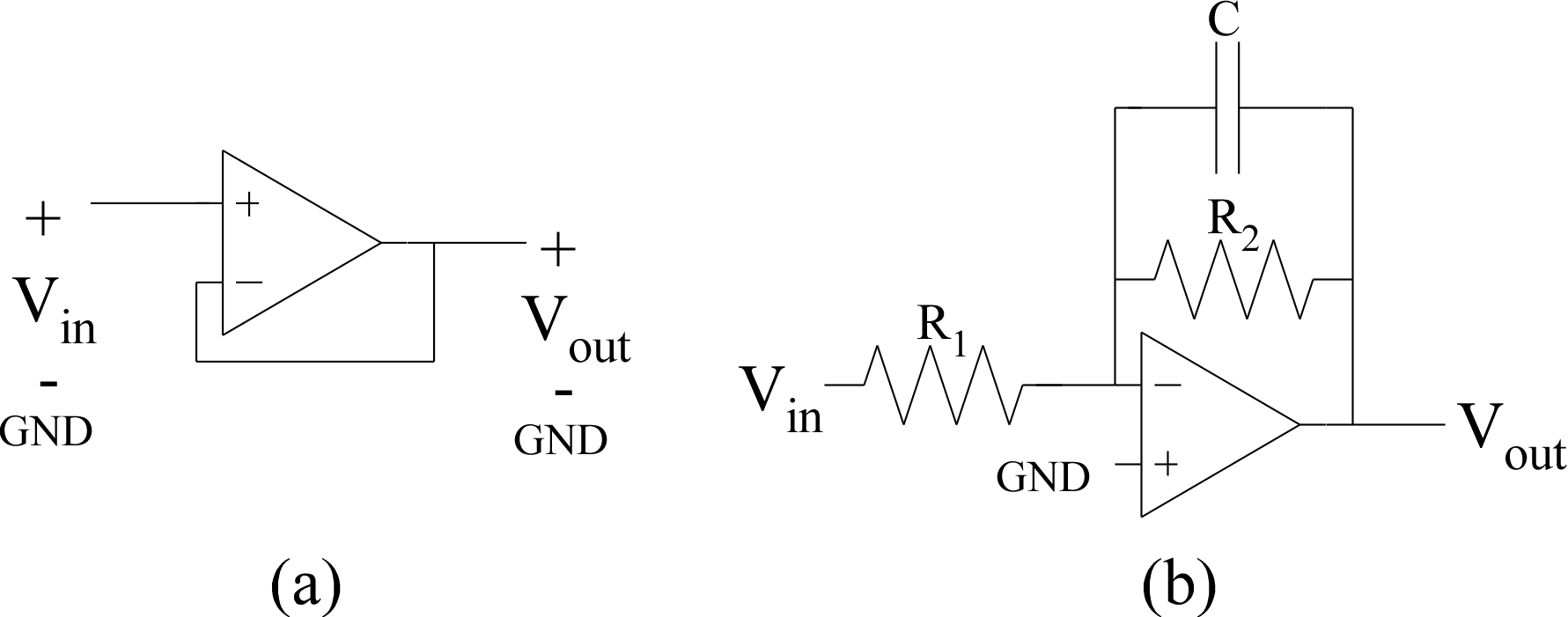
Figure 2: Op-Amp Circuits for lab measurement.
(a) An Op-Amp buffer circuit.
(b) A First-order Op-Amp Resistor--Capacitor Circuit.
|
- Set up the First-Order RC circuit that you find in Fig. 1.
You will want to use an Op-amp buffer (Fig. 2a) between the output and your instrumentation.
First check that the buffer is working, doing a simple sweep of Vin
versus Vout.
Then check that the full circuit is working by doing a simple sweep
of the resistor input voltage vs. Vout.
you will notice that the output voltage should approximately equal the input voltage.
The input voltage can be swept for this measurement between 0 and 3V or 5V.
You should have a gain = 1.
Curve fit this value, and discuss any differences.
- Perform a step response (Fig. 1):
This means you have a square wave input and look at the resulting output voltage.
Put in an input step between 0.5V and 1.5V. You have a dc voltage of 1V.
Analytically solve for the RC timeconstant and for Vout response with time,
as well as use your experimental data to experimentally measure the RC timeconstant.
You will perform a curve fit for the resulting time constant ,
a curve fit to the exponentially decreasing and exponentially increasing data.
Do the two time-constant values agree?
You need to include a plot of the measured data with curve fits for the time-constant of the measured data.
- Frequency response (Fig. 1):
Use your device function to do a frequency sweep.
the device inputs a single frequency and measures the result.
Compare your measured frequency response to your expected result.
- Change resistor, change capacitor value.
Both analytically predict the response and measure
the time-domain response and frequency response.
Compare the analytical values with the devices used.
You will want the step response results and time-constant results
efficiently plotted in your report.
You will want a single plot of the two frequency responses.
- From the components you have available, set up the circuit in Fig. 2 having a low-frequency gain
greater than 3 and a timeconstant within an order of magnitude of Fig. 1.
You should analyze this circuit for its step response and frequency response.
Perform a similar Step response , curve fit for timeconstant,
and Frequency response (one set of resistors)
for this circuit as you did for the circuit in Fig. 1.
|